Exercícios sobre Associação Mista de Resistores
Determine a resistência equivalente entre os terminais A e B da seguinte associação de resistores:
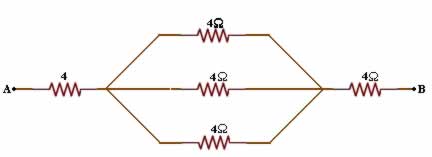
Resolvendo primeiramente a associação em paralelo:
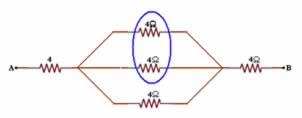
1/Req = 1/4 + 1/4
1/Req = 2/4
Req = 2Ω
Resolvendo a próxima associação em paralelo:
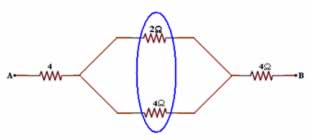
1/Req = 1/2 + 1/4
1/Req = (2 + 1)/4
1/Req = (3/4)Ω
Req = (4/3) Ω
Ao redesenhar o circuito nos deparamos com uma associação em série.

Reqtotal = 4 + 4/3 + 4 = 8 + 4/3 = (24 + 4)/3 = (28/3) = 9,33 Ω
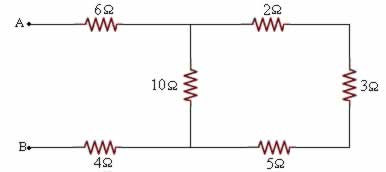
Entre os pontos A e B do circuito abaixo é aplicada uma ddp de 60V.
a. Determine a intensidade de corrente no resistor de 10 Ω.
b. Qual é a ddp entre os extremos do resistor de 6 Ω?
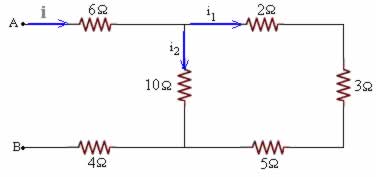
Temos que i = i1 + i2
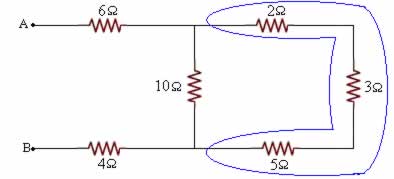
Req1 = 2 + 3 + 5 = 10Ω
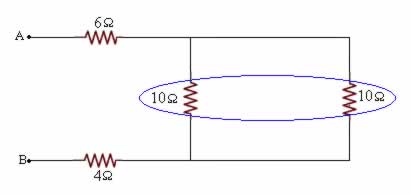
1/Req2 = 1/10 + 1/10
1/Req2 = 2/10
Req2 = 5 Ω
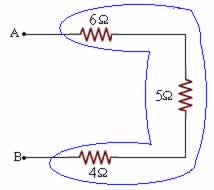
Reqt = 6+ 5 + 4 = 15Ω
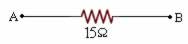
UAB = Reqt.i
60 = 15.i
i = 60/15
i = 4A
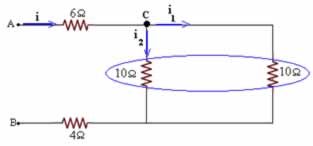
No esquema acima vemos que a corente i se divide em duas ao passar pelo nó c; como os resistores que estão em paralelo são iguais, as correntes que passam por eles também são iguais.
i1 = i2 equação 2
i = i1 + i2 equação 1
Da equação 1 temos que: 4 = i1 + i2
Substituindo, temos 4 = i1 + i1
2i1 = 4
i1 + = 4/2
i1 = 2 A
(OBF) Uma corrente de 0,10ª passa pelo resistor de 25Ω, conforme indicado na figura abaixo. Qual é a corrente que passa pelo resistor de 80 Ω?
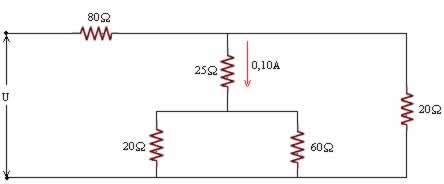
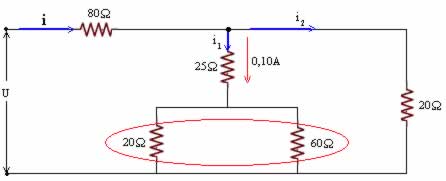
1/Req1 = 1/20 + 1/60 = (3 + 1)/60 = 4/60 = 1/15
Req1 = 15Ω
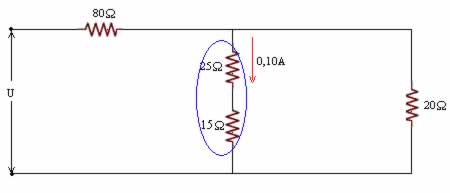
Req2 = 25 + 15 = 40Ω
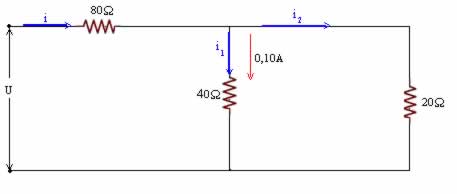
i = i1 + i2
i = 0,10 + i2 equação I
Seja R1 = 40 e R2 = 20, temos que: R1 = 2R2 obs.:*R = U/i
U/i1 = 2.U/i2 Os resistores em questão estão em paralelo, logo a ddp é a mesma para ambos.
i2 = 2.i1 equação II
Substituindo II em I
i = 0,10 + 2.0,10
i = 0,10 + 0,20
i = 0,30 A
Determine a resistência equivalente do seguinte circuito:
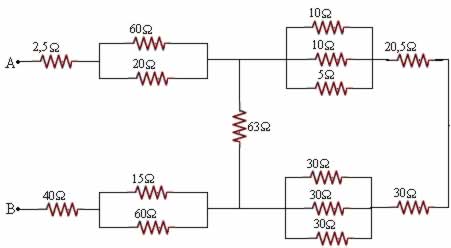
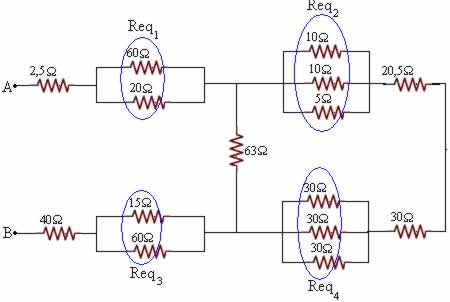
1/Req1 = 1/60 + 1/20 = 1/15
Req1 = 15Ω
1/Req2 = 1/10 + 1/10 + 1/5 = 4/10
Req2 = 2,5Ω
1/Req3 = 1/15 + 1/60 = 5/60
Req3 = 12 Ω
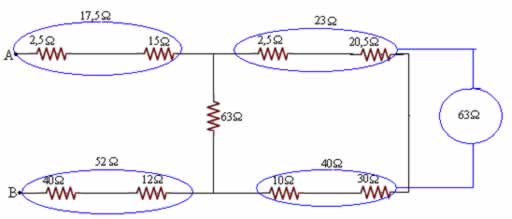
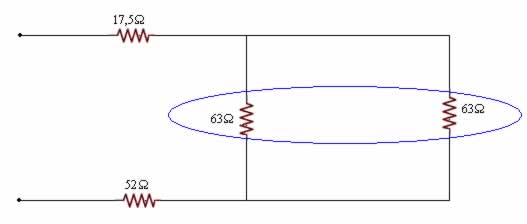
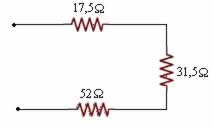
1/Req4 = 1/63 + 1/63 = 2/63
Req4 = 31,5