Exercícios sobre comprimento da circunferência
Uma circunferência possui raio medindo 18 cm. Utilizando π = 3,14, então o comprimento dessa circunferência é:
A) 40,12 cm
B) 56,54 cm
C) 82,28 cm
D) 109,14 cm
E) 112,32 cm
Alternativa E
Calculando o comprimento da circunferência de raio r = 18 e utilizando π = 3,14, temos que:
\(C=2πr\)
\(C=2⋅3,14⋅18\)
\(C=6,24⋅18\)
\(C=112,32\ cm\)
Uma praça possui formato circular com 24 metros de diâmetro. Durante o planejamento do evento de inauguração da praça, o prefeito pediu que fosse foi feita uma cerca em todo o comprimento da circunferência, para controlar a entrada dos visitantes desse evento. Qual é o comprimento mínimo de material necessário para cercar toda a praça?
(Use π = 3)
A) 52 m
B) 64 m
C) 72 m
D) 144 m
E) 162 m
Alternativa C
Como o diâmetro é de 24 metros, então o raio mede 12 metros. Utilizando π = 3, temos que:
\(C=2πr\)
\(C=2⋅3⋅12 \)
\(C=6⋅12 \)
\(C=72\ m\)
Uma região circular possui comprimento medindo 18π cm. Nessas condições, a medida do raio dessa região é igual a:
A) 18 cm
B) 12 cm
C) 9 cm
D) 6 cm
E) 3 cm
Alternativa C
Sabemos que:
\(C=2πr\)
\(18π=2πr\)
\(r=\frac{18π}{2π}\)
\(r=9\ cm\)
Kárita decidiu fazer caminhada todos os dias em volta do parque que tem próximo da sua casa. Esse parque conta com um circuito circular, de raio medindo 42 metros. Se, em determinado dia, ela decide andar no mínimo 5 km, o número mínimo de voltas inteiras que ela deve dar em torno desse circuito é igual a:
(Use π = 3)
A) 21 voltas
B) 20 voltas
C) 19 voltas
D) 18 voltas
E) 17 voltas
Alternativa B
Primeiro calcularemos a distância percorrida a cada volta.
\(C=2πr\)
\(C=2⋅3⋅42\)
\(C=6⋅42\)
\(C=252\ m\)
Agora dividiremos 5 km, que equivale a 5000 metros, por 252 metros.
\(5000∶252=19,8\)
Serão necessárias 20 voltas.
O raio de uma bicicleta possui 28 cm, então o comprimento da roda dessa bicicleta mede:
(Use π = 3)
A) 84 cm
B) 120 cm
C) 146 cm
D) 152 cm
E) 168 cm
Alternativa E
Calculando o comprimento da circunferência, temos que:
\(C=2πr\)
\(C=2⋅3⋅28\)
\(C=6⋅28\)
\(C=168\ cm\)
Durante a construção da sua casa, Natália quis que a piscina tivesse formato de uma circunferência com 62 metros de comprimento. Utilizando 3,1 como aproximação de π, a medida do diâmetro dessa piscina deve ser:
A) 10 metros
B) 12 metros
C) 14 metros
D) 18 metros
E) 20 metros
Alternativa E
\(C=2πr\)
\(62=2⋅3,1⋅r\)
\(62=6,2⋅r\)
\(r=\frac{62}{6,2}\)
\(r=10 \)
Como o raio é 10, então o diâmetro é de 20 metros.
A roda gigante é um brinquedo bastante comum em parques de diversão e costuma encantar pela sua altura. Em um parque, a roda gigante possui diâmetro medindo 52 metros, e todo o seu comprimento será enfeitado com pisca-pisca para o Natal. Para calcular os custos dessa decoração, tornou-se necessário o cálculo do comprimento da circunferência dessa roda gigante. O comprimento dessa roda gigante, em metros, é de:
A) 26π
B) 52π
C) 104π
D) 157π
E) 202π
Alternativa B
Sabemos que \(C=2πr\); mas 2r = d. Então temos que:
\(C=dπ\)
\(C=52π\)
Uma região formada por um semicírculo possui diâmetro medindo 4 metros. Qual é a medida do contorno dessa região?
(Use π = 3)
A) 8 m
B) 10 m
C) 12 m
D) 14 m
E) 16 m
Alternativa B
Essa região possui contorno igual à medida do diâmetro mais o comprimento de uma semicircunferência. Sabemos que o comprimento da circunferência é 2πr, então a metade dele é πr. Como o diâmetro mede 4 cm, então o raio mede 2, logo, temos que:
\(C=πr+4 \)
\(C=3⋅2+4\)
\(C=6+4\)
\(C=10\ m\)
Priscilla decidiu realizar caminhadas semanalmente em torno da praça em frente a sua casa. Essa praça possui formato circular, com raio medindo 25 metros. A meta de Priscilla é andar 18.000 km durante a semana, sendo que ela não caminhará aos sábados e aos domingos. Supondo que ela decida caminhar a mesma quantidade de km por dia para atingir a sua meta, o número de voltas que ela fará nessa praça será igual a:
(Use π = 3)
A) 12 voltas
B) 18 voltas
C) 24 voltas
D) 30 voltas
E) 36 voltas
Alternativa C
Calcularemos primeiro o comprimento da circunferência da praça:
\(C=2πr\)
\(C=2⋅3⋅25\)
\(C=6⋅25\)
\(C=150 \)
Sabendo que uma volta possui 150 metros e calculando a divisão:
18.000 : 150 = 24 voltas
(Enem) A figura é uma representação simplificada do carrossel de um parque de diversões, visto de cima. Nessa representação, os cavalos estão identificados pelos pontos escuros, e ocupam circunferências de raios 3 m e 4 m respectivamente, ambas centradas no ponto O. Em cada sessão de funcionamento, o carrossel efetua 10 voltas.
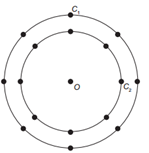
Quantos metros uma criança sentada no cavalo \(C_1\) percorrerá a mais do que uma criança no cavalo \(C_2\), em uma sessão? Use 3,0 como aproximação para S.
A) 55,5
B) 60,0
C) 175,5
D) 235,5
E) 240,0
Alternativa B
Calcularemos o comprimento \(C_1\):
\(10C_1=10⋅2⋅3⋅4=240\ m\)
\(10C_2=C_2=10⋅2⋅3⋅3=180\ m\)
A diferença entre esses comprimentos é de:
\(240-180=60\)
(Enem) Um homem, determinado a melhorar sua saúde, resolveu andar diariamente numa praça circular que há em frente à sua casa. Todos os dias ele dá exatamente 15 voltas em torno da praça, que tem 50 m de raio. Use 3 como aproximação para π.
Qual é a distância percorrida por esse homem em sua caminhada diária?
A) 0,30 km
B) 0,75 km
C) 1,50 km
D) 2,25 km
E) 4,50 km
Alternativa E
Primeiro calcularemos o comprimento da circunferência:
\(C=2πr\)
\(C=2⋅3⋅50 \)
\(C=300 \)
Sabendo que o comprimento é 300 metros, então, ao dar 15 voltas, a distância percorrida será de:
\(15⋅300=4500=4,5\ km\)
(Enem) Uma empresa que organiza eventos de formatura confecciona canudos de diplomas a partir de folhas de papel quadradas. Para que todos os canudos fiquem idênticos, cada folha é enrolada em torno de um cilindro de madeira de diâmetro d em centímetros, sem folga, dando-se 5 voltas completas em torno de tal cilindro. Ao final, amarra-se um cordão no meio do diploma, bem ajustado, para que não ocorra o desenrolamento, como ilustrado na figura:

Em seguida, retira-se o cilindro de madeira do meio do papel enrolado, finalizando a confecção do diploma. Considere que a espessura da folha de papel original seja desprezível.
Qual é a medida, em centímetros, do lado da folha de papel usado na confecção do diploma?
A) π d
B) 2π d
C) 4π d
D) 5π d
E) 10π d
Alternativa D
Sabemos que o lado da folha tem comprimento igual à base do cilindro, que é um círculo. Como o raio é igual à metade do diâmetro, e serão dadas 5 voltas, então temos que:
\(5C=2πr⋅5\)
\(5C=2π⋅\frac{d}2⋅5\)
\(5C=5π\ d\)






